La covarianza e le sue principali proprietà
Vuoi sapere tutto sulla covarianza e sul coefficiente di correlazione lineare, sulle loro proprietà, sugli indici di connessione, di concordanza, di associazione, di dipendenza in media? A fine pagina trovi il link al formulario completo!
La definizione di covarianza
Dati due caratteri quantitativi (o variabili quantitative) X e Y, indicando con M[…] la media aritmetica della variabile in parentesi, con MX la media aritmetica di X, con MY la media aritmetica di Y, con MXY la media aritmetica di XY, con xi la modalità i-esima di X, con yj la modalità j-esima di Y, con nij la frequenza congiunta di (xi,yj), con k il numero di modalità di X, con h il numero di modalità di Y e con N il numero di unità statistiche osservate.
- Formula generale:
![]()
- Formula per una distribuzione di frequenza:
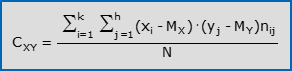 Se CXY > 0, si parla di correlazione lineare positiva tra X ed Y. Le coppie di osservazioni di X ed Y nelle N unità statistiche tendono a disporsi intorno ad una retta con pendenza positiva (in altri termini, X ed Y tendono a muoversi in modo proporzionale e concorde). Se CXY < 0, si parla di correlazione lineare negativa tra X ed Y. Le coppie tendono a disporsi intorno ad una retta con pendenza negativa (X ed Y tendono a muoversi in modo proporzionale ma discorde). Se CXY = 0, si parla di incorrelazione lineare tra X ed Y. Le coppie non mostrano alcuna tendenza ad allinearsi intorno ad una retta. La covarianza è alla base della definizione e del calcolo del coefficiente di correlazione lineare di Bravais-Pearson. In effetti, ρXY è il rapporto tra CXY ed il prodotto tra le deviazioni standard di X e di Y.
Se CXY > 0, si parla di correlazione lineare positiva tra X ed Y. Le coppie di osservazioni di X ed Y nelle N unità statistiche tendono a disporsi intorno ad una retta con pendenza positiva (in altri termini, X ed Y tendono a muoversi in modo proporzionale e concorde). Se CXY < 0, si parla di correlazione lineare negativa tra X ed Y. Le coppie tendono a disporsi intorno ad una retta con pendenza negativa (X ed Y tendono a muoversi in modo proporzionale ma discorde). Se CXY = 0, si parla di incorrelazione lineare tra X ed Y. Le coppie non mostrano alcuna tendenza ad allinearsi intorno ad una retta. La covarianza è alla base della definizione e del calcolo del coefficiente di correlazione lineare di Bravais-Pearson. In effetti, ρXY è il rapporto tra CXY ed il prodotto tra le deviazioni standard di X e di Y.
Le proprietà della covarianza
Alcune delle principali proprietà sono:
- La covarianza, in modulo, è minore o uguale al prodotto tra le deviazione standard di X, SX, e di Y, SY:
![]()
- Se Y=a+bX, cioè se X ed Y sono legati da una relazione lineare perfetta, la covarianza è pari ad uno dei suoi valori estremi e precisamente è pari al prodotto tra le deviazioni standard di X e di Y, con lo stesso segno del coefficiente angolare b. Viceversa, se la covarianza raggiunge uno dei suoi valori estremi, X ed Y sono legati da una relazione lineare perfetta. Se CXY = ±SXSY si parla di correlazione lineare perfetta (rispettivamente, positiva e negativa):

- La covarianza tra X ed Y è uguale a quella tra Y ed X (invarianza rispetto all’ordine dei caratteri):
![]()
- La covarianza tra X e se stesso è uguale alla varianza di X, VX:
![]()
- La covarianza tra funzioni lineari di X ed Y è uguale a quella tra X ed Y, moltiplicata per i coefficienti angolari delle funzioni:
![]()
Login / Registrati
Vai al formulario
I formulari dell’area
STATISTICA DESCRITTIVA
[2] – [3] – [4] – [5] – [6] – [7] – [8]
Vuoi spiegazioni dettagliate sulle formule ed i risultati presentati nel formulario, corredate da esempi, esercizi ed applicazioni? Trovi tutto questo nelle nostre videolezioni sulle Relazioni statistiche.
Videolezioni Relazioni statistiche
Vuoi preparare un esame di Statistica con MOV? Clicca sul pulsante Cosa devi studiare?, riempi il form ed inviaci il tuo programma: ti suggeriremo un piano di studio basato sui nostri strumenti didattici e calibrato sulle tue esigenze.
