La variabile casuale Normale o Gaussiana ed il teorema limite centrale
Vuoi sapere tutto sulle variabili casuali continue, sui loro momenti, le loro proprietà, sul teorema limite centrale e la legge dei grandi numeri ed ancora sui modelli di variabile Uniforme, Gaussiana, Lognormale, Beta, Esponenziale negativa e Gamma? A fine pagina trovi il link al formulario completo!
La variabile casuale Normale o Gaussiana
Una variabile casuale X si dice Normale o Gaussiana se ha le seguenti caratteristiche:
- Il supporto di X, cioè l’insieme dei valori che X può assumere, coincide con la retta reale:
![]()
- La funzione di densità di probabilità di X vale:
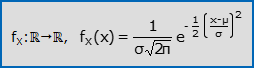 dove μ e σ>0 sono parametri reali. Il grafico di fX(x) è noto come curva Normale o curva Gaussiana o semplicemente Gaussiana, di parametri μ e σ: è una curva campanulare simmetrica rispetto a μ, che è l’unico punto di massimo; è concava in (μ-σ, μ+σ), convessa altrove e tende a 0 nelle code, ovvero per x che tende a ±∞; a parità di σ, aumenti di μ traslano la curva verso destra; a parità di μ, aumenti di σ riducono l’area (= probabilità) intorno a μ ed aumentano l’area nelle code.
dove μ e σ>0 sono parametri reali. Il grafico di fX(x) è noto come curva Normale o curva Gaussiana o semplicemente Gaussiana, di parametri μ e σ: è una curva campanulare simmetrica rispetto a μ, che è l’unico punto di massimo; è concava in (μ-σ, μ+σ), convessa altrove e tende a 0 nelle code, ovvero per x che tende a ±∞; a parità di σ, aumenti di μ traslano la curva verso destra; a parità di μ, aumenti di σ riducono l’area (= probabilità) intorno a μ ed aumentano l’area nelle code.
La funzione di ripartizione di X si ottiene integrando la densità – FX(x) = ∫ (-∞,x] fX(t)dt – secondo la regola generale, ma non ammette una forma analitica esplicita.
- Il valore atteso e la varianza di X valgono:
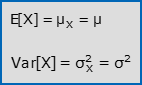 dal che segue che i parametri μ e σ hanno il significato, rispettivamente, di media e deviazione standard di X.
dal che segue che i parametri μ e σ hanno il significato, rispettivamente, di media e deviazione standard di X.
- I coefficienti di asimmetria e di curtosi valgono:
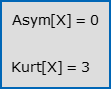 X è simmetrica; Kurt[X] = 3 è il valore di riferimento per giudicare la curtosi di una variabile casuale Y qualsiasi, che in effetti misura il minore o maggiore appuntimento (ed il maggiore o minore ispessimento delle code) della densità di Y rispetto alla Gaussiana; nel primo caso sarà Kurt[Y]<3 ed Y si dirà platicurtica o iponormale, nel secondo sarà Kurt[Y]>3 ed Y si dirà leptocurtica o ipernormale.
X è simmetrica; Kurt[X] = 3 è il valore di riferimento per giudicare la curtosi di una variabile casuale Y qualsiasi, che in effetti misura il minore o maggiore appuntimento (ed il maggiore o minore ispessimento delle code) della densità di Y rispetto alla Gaussiana; nel primo caso sarà Kurt[Y]<3 ed Y si dirà platicurtica o iponormale, nel secondo sarà Kurt[Y]>3 ed Y si dirà leptocurtica o ipernormale.
Per indicare che X è una variabile casuale Normale o Gaussiana, si utilizzano spesso notazioni come X∼N(μ,σ) o X∼N(μ,σ2) o simili (nota: quando i parametri sono numeri, è importante specificare se il secondo rappresenta la varianza o la deviazione standard di X).
- se X∼N(μ,σ) e si definisce Z=(X-μ)/σ, allora Z∼N(0,1); questa trasformazione è nota come standardizzazione di X e la variabile casuale Z dicesi Normale o Gaussiana standard; permette di ricondurre il calcolo di una qualsiasi probabilità associata ad X (quindi, dipendente dai parametri μ e σ) al calcolo di probabilità associate a Z, che non dipendono da alcun parametro e sono disponibili in apposite tavole statistiche. La procedura di calcolo è la seguente:
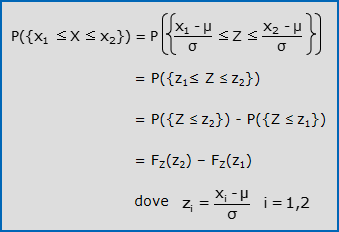 dove x1 e x2 sono numeri reali con x1<x2 ed FZ(x) è la funzione di ripartizione di Z, che è stata appunto ampiamente tabulata; z1 e z2 si dicono scarti standardizzati di x1 e x2; nota che se x1=-∞, allora z1=-∞ e se x2=+∞, allora z2=+∞.
dove x1 e x2 sono numeri reali con x1<x2 ed FZ(x) è la funzione di ripartizione di Z, che è stata appunto ampiamente tabulata; z1 e z2 si dicono scarti standardizzati di x1 e x2; nota che se x1=-∞, allora z1=-∞ e se x2=+∞, allora z2=+∞.
Il teorema limite centrale
La variabile Normale o Gaussiana è centrale in Probabilità come in Statistica, per varie ragioni; una delle principali è che si presta bene a modellare il comportamento probabilistico di molti fenomeni fisici, biologici, sociali, economici, ecc. e questo si spiega, in buona parte, con una sua proprietà espressa nel celebre teorema limite centrale, che qui enunciamo nella sua versione più semplice (v. formulario per estensioni e conseguenze).
Sia (Xk) k=1,2,… una successione di variabili casuali indipendenti e sia Z∼N(0,1); supponi (ipotesi di Lindeberg-Lévy) che queste variabili siano identicamente distribuite, cioè abbiano tutte la stessa media μ e la stessa varianza finita σ2<∞. Vale allora il seguente teorema:
 In sostanza, dalla successione assegnata si ricava la successione delle somme standardizzate, o delle medie standardizzate, delle prime j variabili (j=1,2,…), la quale converge in distribuzione alla Normale standard; in parole povere, ciò significa che la funzione di ripartizione della somma/media standardizzata, all’aumentare di j, tende a ricalcare la curva Gaussiana standardizzata.
In sostanza, dalla successione assegnata si ricava la successione delle somme standardizzate, o delle medie standardizzate, delle prime j variabili (j=1,2,…), la quale converge in distribuzione alla Normale standard; in parole povere, ciò significa che la funzione di ripartizione della somma/media standardizzata, all’aumentare di j, tende a ricalcare la curva Gaussiana standardizzata.
Nota che il risultato non dipende dalla funzione di ripartizione delle variabili di partenza. Pertanto, se un dato fenomeno è il risultato di una somma o di una media di tanti fattori indipendenti (e con la stessa distribuzione, ma questa ipotesi si può eliminare o almeno attenuare), la sua struttura probabilistica sarà approssimativamente Normale, a prescindere dalla struttura probabilistica dei singoli fattori che lo determinano.
Login / Registrati
Vai al formulario
I formulari dell’area
PROBABILITA’
[1] – [2] – [3] – [4]
Vuoi spiegazioni dettagliate sulle formule ed i risultati presentati nel formulario, corredate da esempi, esercizi ed applicazioni? Trovi tutto questo nelle nostre videolezioni sulle Variabili casuali continue.
Videolezioni Variabili casuali continue
Vuoi preparare un esame di Statistica con MOV? Clicca sul pulsante Cosa devi studiare?, riempi il form ed inviaci il tuo programma: ti suggeriremo un piano di studio basato sui nostri strumenti didattici e calibrato sulle tue esigenze.
