Variabili casuali discrete

La variabile casuale Binomiale conta i “successi” in n prove indipendenti

Vuoi sapere tutto sulle variabili casuali discrete, sui loro momenti, le loro proprietà e sulle caratteristiche dei modelli Uniforme, Bernoulli, Binomiale, Binomiale relativo, Poisson, Ipergeometrico, Geometrico e Binomiale negativo? A fine pagina trovi il link al formulario completo!

La variabile casuale di Bernoulli

Considera la prova o esperimento casuale che consiste nel verificarsi (“successo”) o meno (“insuccesso”) di un evento incerto E, in determinate condizioni. Sia p la probabilità di successo, p = P(E), secondo una misura di probabilità P; per evitare casi degeneri, supponi sia 0<p<1. Immagina di codificare il successo con l’1 e l’insuccesso con lo 0; allora questa prova – detta di Bernoulli – è descritta dalla variabile casuale di Bernoulli, X, avente le seguenti caratteristiche:

• Il supporto di X, cioè l’insieme dei valori che X può assumere, è formato dai numeri 0 ed 1:

• La funzione di probabilità di X assegna all’1 la probabilità di successo p ed allo 0 la probabilità di insuccesso 1-p:

• La funzione di ripartizione di X è nulla prima dello 0, vale 1 dopo l’1 e vale 1-p tra 0 ed 1:

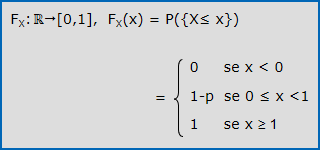
• Il valore atteso e la varianza di X valgono:

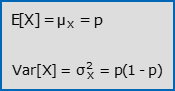
• I coefficienti di asimmetria e di curtosi di X valgono:

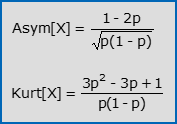così che X risulta asimmetrica per p≠1/2, leptocurtica per valori di p vicini agli estremi 0 ed 1, platicurtica per valori di p vicini ad 1/2.

Per indicare che X è una variabile casuale di Bernoulli di parametro p, si utilizzano spesso notazioni come X∼Ber(p) o simili.

Le variabili casuali Binomiale e Binomiale relativa

Considera la prova o esperimento casuale che consiste nel contare quante volte un evento incerto E si è verificato (“successo”) in n sottoprove di Bernoulli indipendenti, in ognuna delle quali la probabilità di successo è p = P(E); sempre per evitare casi degeneri, continua a supporre 0<p<1. L’aggettivo “indipendenti” allude al fatto che il risultato di ciascuna sottoprova, una volta noto, non modifica la probabilità di successo nelle altre sottoprove. L’esperimento in questione è descritto dalla variabile casuale Binomiale, X, avente le seguenti caratteristiche:

• Il supporto di X, cioè l’insieme dei valori che X può assumere, è formato dai numeri interi tra 0 ed n:

• La funzione di probabilità di X vale:

Il numero pⁱ(1-p)^n-i esprime la probabilità di una specifica sequenza di i successi ed n-i insuccessi; il numero C_n,i = n!/[i!(n-i)!] è il coefficiente binomiale n su i e conta il numero di possibili sequenze con i successi ed n-i insuccessi; pertanto, f_X(i) è la probabilità di i successi (in ordine qualsiasi) in n prove. La funzione di ripartizione di X si ottiene per somma della funzione di probabilità, F_X(x) = Σ_{i ≤ x} f_X(i), secondo la regola generale, ma non ammette una forma analitica esplicita.

• Il valore atteso e la varianza di X valgono:

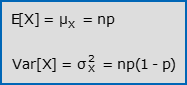
• I coefficienti di asimmetria e di curtosi di X valgono:

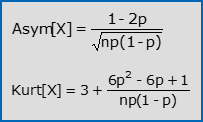così che X risulta asimmetrica per p≠1/2, leptocurtica per valori di p vicini agli estremi 0 ed 1, platicurtica per valori di p vicini ad 1/2.

Per indicare che X è una variabile casuale Binomiale di parametri n e p, si utilizzano spesso notazioni come X∼Bin(n,p) o simili.

Molti di questi ed altri risultati (v. formulario) si deducono abbastanza facilmente dal fatto che X si può esprimere come somma di n variabili di Bernoulli – X_i∼Ber(p)  i=1,2,.., n – ciascuna delle quali descrive una delle sottoprove; l’indipendenza delle sottoprove si traduce nell’indipendenza delle variabili X_i; in sintesi, quindi, la Binomiale si può riguardare come somma di n variabili di Bernoulli di parametro p indipendenti.

Se X∼Bin(n,p), la variabile casuale Y=X/n si chiama Binomiale relativa ed esprime la quota di successi nelle n sottoprove indipendenti. Il suo supporto è formato dalle frazioni 0/n, 1/n,…,n/n; la funzione di probabilità è f_Y(i/n) = f_X(i); risulta inoltre E[Y] = p e Var[Y]=p(1-p)/n, mentre i coefficienti di asimmetria e di curtosi coincidono con quelli di X.

Login / Registrati
Vai al formulario

I formulari dell’area
PROBABILITA’
[1] – [2] – [3] – [4]

Vuoi spiegazioni dettagliate sulle formule ed i risultati presentati nel formulario, corredate da esempi, esercizi ed applicazioni? Trovi tutto questo nelle nostre videolezioni sulle Variabili casuali discrete.

                   Videolezioni                    Variabili casuali discrete

Vuoi preparare un esame di Statistica con MOV? Clicca sul pulsante Cosa devi studiare?, riempi il form ed inviaci il tuo programma: ti suggeriremo un piano di studio basato sui nostri strumenti didattici e calibrato sulle tue esigenze.

Cosa devi studiare?