Media ponderata aritmetica, quadratica, armonica, geometrica, di potenze
Vuoi sapere tutto sulla media ponderata di una serie statistica, sulle sue proprietà, sul calcolo della media quando i dati sono organizzati in una distribuzione di frequenza? A fine pagina trovi il link al formulario completo!
Le principali medie ponderate
Sia X un carattere quantitativo (o variabile quantitativa) osservato su N unità statistiche e siano x1, x2,…,xN le osservazioni. Siano p1, p2,…,pN numeri non negativi, detti pesi delle osservazioni, e sia p la somma positiva di tali numeri (il numero pi(r) = pi/p si dice peso relativo dell’osservazione xi, i=1,2,…,N):
- La media ponderata (o pesata) aritmetica di X è la somma delle osservazioni, moltiplicate per i rispettivi pesi relativi:
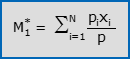
- La media ponderata (o pesata) quadratica di X è la radice quadrata della media ponderata aritmetica delle osservazioni al quadrato:
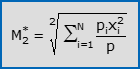
- La media ponderata (o pesata) armonica di X è il reciproco della media ponderata aritmetica dei reciproci delle osservazioni:
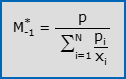
- La media ponderata (o pesata) geometrica di X è il prodotto tra le osservazioni elevate ai rispettivi pesi relativi; ovvero, equivalentemente, è l’esponenziale della media ponderata aritmetica dei logaritmi naturali delle osservazioni:
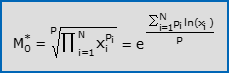
- La media ponderata (o pesata) di potenze di ordine r di X è la radice r-esima della media ponderata aritmetica delle osservazioni a potenza r:
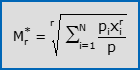 Note:
Note:
- Nel caso particolare in cui i pesi sono tutti uguali ad 1 (e quindi p=N), le formule precedenti definiscono altrettante medie semplici di X
- La media armonica è definita solo se le osservazioni e la somma che compare a denominatore sono diverse da 0
- La media geometrica è definita sole se le osservazioni sono positive; la seconda formula in genere ne semplifica il calcolo
- La media di potenze di ordine r è definita, in generale, solo se le osservazioni sono positive ed r è diverso da 0; per r=1, si riduce alla media aritmetica, per r=-1 alla media armonica, per r=2 alla media quadratica mentre il valore limite per r che tende a 0 coincide con la media geometrica
- Se all'(α/2)% delle osservazioni più piccole ed all'(α/2)% delle osservazioni più grandi si assegnano pesi pari a 0, si ottengono le così dette medie tagliate (trimmed mean) di ordine α di X (in genere il concetto si applica alla media aritmetica)
Tutte queste medie godono di numerose ed importanti proprietà (vedi formulario); a titolo di esempio, si può provare che la media armonica non supera mai quella geometrica, che non supera mai quella aritmetica, che non supera mai quella quadratica, con l’uguaglianza che si realizza soltanto nel caso degenere in cui tutte le N osservazioni coincidono.
Login / Registrati
Vai al formulario
I formulari dell’area
STATISTICA DESCRITTIVA
[2] – [3] – [4] – [5] – [6] – [7] – [8]
Vuoi spiegazioni dettagliate sulle formule ed i risultati presentati nel formulario, corredate da esempi, esercizi ed applicazioni? Trovi tutto questo nelle nostre videolezioni sulle Medie analitiche.
Vuoi preparare un esame di Statistica con MOV? Clicca sul pulsante Cosa devi studiare?, riempi il form ed inviaci il tuo programma: ti suggeriremo un piano di studio basato sui nostri strumenti didattici e calibrato sulle tue esigenze.
