Distribuzioni e serie statistiche

Distribuzioni di frequenza assoluta, relativa, percentuale, cumulata

Vuoi sapere tutto sulle distribuzioni di frequenza assoluta, relativa, percentuale, cumulata, semplici e doppie, sulle distribuzioni di intensità e sulle serie statistiche? A fine pagina trovi il link al formulario completo!

Le distribuzioni semplici di frequenza

Sia X un carattere (o variabile) osservato su N unità statistiche. Supponi che X abbia k modalità (valori) ed indica con x_i la modalità i-esima (i=1,2,…,k). Potrebbero anche essere classi di modalità, in tal caso la notazione è [x_i, x_i+1) o simile.

• La frequenza assoluta di x_i è il numero n_i di unità statistiche sulle quali hai osservato x_i. Una tabella che elenca le k modalità di X insieme alle rispettive frequenze assolute, si chiama distribuzione semplice di frequenza assoluta di X. Segue una notazione compatta per tale tabella.

• La frequenza relativa di x_i è la quota n_i/N di unità statistiche sulle quali hai osservato x_i. Una tabella che elenca le k modalità di X insieme alle rispettive frequenze relative, si chiama distribuzione semplice di frequenza relativa di X. Segue una notazione compatta per tale tabella.

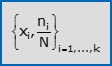
• La frequenza percentuale di x_i è la percentuale n_i·(100/N) di unità statistiche sulle quali hai osservato x_i. Una tabella che elenca le k modalità di X insieme alle rispettive frequenze percentuali, si chiama distribuzione semplice di frequenza percentuale di X. Segue una notazione compatta per tale tabella.

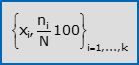Se il carattere X è ordinabile e si suppongono ordinate in modo crescente le sue modalità, a partire dalle precedenti distribuzioni si possono costruire le corrispondenti distribuzioni di frequenza cumulata. In particolare:

• Si chiama frequenza assoluta [risp. relativa, percentuale] cumulata di x_iil numero n₁+n₂+…+n_i [risp. la quota (n₁+n₂+…+n_i)/N, la percentuale (n₁+n₂+…+n_i)·(100/N)] di unità statistiche sulle quali si è osservato una modalità non superiore a x_i. Notazioni compatte per le corrispondenti distribuzioni semplici di frequenza cumulata sono:

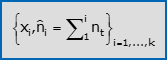
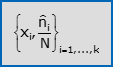
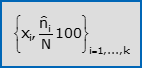
Le distribuzioni doppie di frequenza

Siano X ed Y caratteri (o variabili) osservati su N unità statistiche. Supponi che X abbia k possibili modalità (o valori) ed indica con x_i la modalità i-esima (i=1,2,…,k) e che Y abbia h possibili modalità (o valori) ed indica con y_j la modalità j-esima (j=1,2,…,h). Sia per X che per Y al posto delle modalità puntuali potresti avere classi di modalità.

• La frequenza assoluta [risp. relativa, percentuale] congiunta della coppia (x_i,y_j) è il numero n_ij [risp. la quota n_ij/N, la percentuale n_ij·(100/N)] di unità statistiche sulle quali hai osservato sia x_i che y_j. Una tabella che elenca in riga le k modalità di X, in colonna le h modalità di Y e associa ad ogni coppia di modalità la sua frequenza assoluta [risp. relativa, percentuale] congiunta, si chiama distribuzione doppia di frequenza assoluta [risp. relativa, percentuale] congiunta di (X,Y); una notazione compatta per tale tabella è:

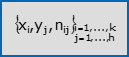
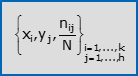
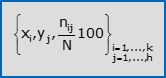
Se i caratteri X ed Y sono entrambi ordinabili e si suppongono ordinate in modo crescente le rispettive modalità, a partire dalle precedenti distribuzioni si possono costruire le corrispondenti distribuzioni di frequenza cumulata. In particolare:

• La frequenza assoluta cumulata congiunta di (x_i,y_j) è il numero (n₁₁+n₁₂+…+n_1j)+(n₂₁+n₂₂+…+n_2j)+…+(n_i1+n_i2+…+n_ij) di unità statistiche sulle quali hai osservato una modalità non superiore a x_i ed una modalità non superiore ad y_j. Tale numero, diviso per N, dà la frequenza relativa cumulata congiunta di (x_i,y_j). Moltiplicato invece per 100/N dà la frequenza percentuale cumulata congiunta di (x_i,y_j). Seguono notazioni compatte per le corrispondenti distribuzioni doppie di frequenza cumulata congiunta.

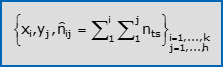
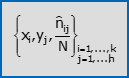
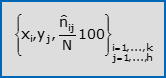
Login / Registrati
Vai al formulario

I formulari dell’area
STATISTICA DESCRITTIVA
[2] – [3] – [4] – [5] – [6] – [7] – [8]

Vuoi spiegazioni dettagliate sulle formule ed i risultati presentati nel formulario, corredate da esempi, esercizi ed applicazioni? Trovi tutto questo nelle nostre videolezioni sulle Distribuzioni e serie statistiche.

                   Videolezioni                    Distribuzioni e serie statistiche

Vuoi preparare un esame di Statistica con MOV? Clicca sul pulsante Cosa devi studiare?, riempi il form ed inviaci il tuo programma: ti suggeriremo un piano di studio basato sui nostri strumenti didattici e calibrato sulle tue esigenze.

Cosa devi studiare?