Tra Geometria ed Analisi: Calcolo Integrale e un po’ di fantasia
Per rivedere il testo del problema clicca qui. Su MOV, nelle nostre videolezioni, abbiamo discusso tutti gli strumenti necessari a risolvere questo problema; servono un po’ di Calcolo Integrale – in particolare, le proprietà geometriche ed alcune proprietà algebriche dell’integrale – un po’ di Calcolo Differenziale ed un po’…di fantasia!
Videolezioni Calcolo Integrale Videolezioni Calcolo Differenziale
LA SOLUZIONE IN SINTESI
LA SOLUZIONE IN DETTAGLIO
Il significato geometrico dell’integrale
Partiamo dalla conformazione del parco: i suoi confini sono la linea orizzontale rossa e la curva verde scuro. In termini matematici, puoi pensare la linea rossa come asse delle ascisse di un sistema cartesiano avente per asse delle ordinate il lato sinistro della mappa; e la curva verde come grafico di una funzione f(x) continua, tracciato rispetto al sistema cartesiano (nota che qualsiasi retta parallela all’asse delle ordinate, incontra la curva verde in un solo punto: questo requisito è indispensabile per poter interpretare la curva verde come grafico di una funzione).
L’area sottesa al grafico di f(x) in un intervallo è misurata dall’integrale di f(x) nell’intervallo. Si tratta però di un’aera “con segno”: cioè la parte nel semipiano positivo (sopra la linea rossa) si conta con segno “+”, mentre quella nel semipiano negativo (sotto la linea rossa) con segno “-“. Questo ti permette di scrivere il profitto generato dall’affare, in funzione di x. Infatti, le aree del parco sopra la linea rossa danno ricavi per 1,5€/km2 al giorno (differenza tra costo del biglietto e costo di gestione), mentre le aree sotto la linea rossa danno costi per 1,5€/km2; poiché nella funzione di profitto i ricavi entrano col “+” ed i costi col “-“, affittando il terreno fino ad x, il profitto P(x) sarà:
![]()
Il secondo addendo a destra dell’uguale tiene conto del costo di affitto del terreno: il canone di 0,45€/km2 si applica all’intera superficie affittata, un rettangolo di area 20·x.
Derivare una funzione integrale
Ora devi massimizzare P(x), sapendo che x può variare tra 0 e 50, estremi inclusi; ovviamente x=0 equivale a rifiutare l’affare mentre x=50 equivale ad affittare l’intero terreno disponibile. Se escludi per un attimo questi valori estremi e limiti l’attenzione all’intervallo (0, 50), puoi massimizzare P(x) studiando il segno della sua derivata. Qui ti aiuta il teorema fondamentale del Calcolo Integrale, che ti permette di derivare la funzione integrale che compare in P(x); a conti fatti:
P'(x) = 1,5·f(x)-9
Pertanto, P'(x)>0 (cioè P(x) cresce) dove f(x)>6 e P'(x)<0 (cioè P(x) decresce) dove f(x)<6. Se indichi con a, b e c le ascisse dei punti di intersezione tra la retta y=6 (linea rossa tratteggiata) e la funzione f(x), puoi concludere che:
P(x) decresce tra 0 ed a; cresce tra a e b; decresce tra b e c; cresce tra c e 50
Le proprietà algebriche dell’integrale
Per il punto di massimo assoluto hai tre candidati: uno interno, cioè x=b; e due di frontiera, cioè x=0 ed x=50. In quale di questi punti P(x) vale di più? Ovvero, qual è più grande tra P(0), P(b) e P(50)? Movy risponde P(b) e ne dà una parziale dimostrazione, provando che P(b)>P(0)=0. La dimostrazione si basa sulla possibilità di riscrivere P(b)>0 nel modo seguente:
![]()
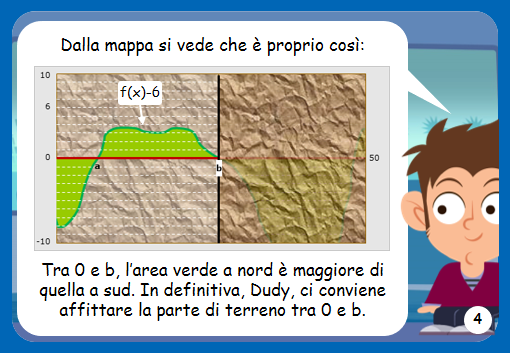
L’ultima disequazione è verificata se l’area “con segno” sottesa alla funzione f(x)-6, nell’intervallo (0,b), è positiva. La funzione f(x)-6 non è altro che f(x) “abbassata” di 6 unità, come nel grafico del box 4; con riferimento a tale grafico, la disequazione si può tradurre dicendo che l’area verde sopra la linea rossa (che ha segno “+”) deve essere maggiore dell’area verde sotto la linea rossa (che ha segno “-“). Dalla mappa si vede che le cose stanno proprio così: quindi, P(b)>0.
Movy lascia a Dudy il compito di dimostrare che P(b)>P(50). La logica della dimostrazione è analoga alla precedente. Con alcuni passaggi che sfruttano le proprietà dell’integrale, la disequazione diventa:
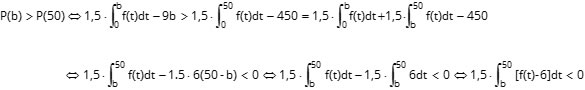
L’ultima disequazione è verificata se l’area “con segno” sottesa alla funzione f(x)-6, nell’intervallo (b,50), è negativa; una volta “abbassata” di 6 unità la funzione f(x), potrai osservare facilmente che l’area verde sopra la linea rossa è minore dell’area verde sotto la linea rossa; quanto a dire che la disuguaglianza è soddisfatta e quindi P(b)>P(50).
Soluzione del problema
P(x) raggiunge il suo massimo assoluto in x=b; inoltre, P(b)>0; a Movy e Dudy quindi conviene affittare il terreno compreso tra 0 e b. La soluzione trovata è assolutamente rigorosa anche se geometrica; per calcolare b dovresti conoscere la forma analitica di f(x) e risolvere l’equazione f(x)=6; tale equazione ha due soluzioni reali, la più grande delle quali è proprio b. Alternativamente, con una buona mappa, potresti stimare il punto b con i comuni strumenti di misurazione.
PROBLEMA #5 — SOLUZIONE #5
PROBLEMA #7 — SOLUZIONE #7
Vuoi preparare un esame di Matematica con MOV? Clicca sul pulsante Cosa devi studiare?, riempi il form ed inviaci il tuo programma: ti suggeriremo un piano di studio basato sui nostri strumenti didattici e calibrato sulle tue esigenze.