Rapporti statistici

I numeri indice per misurare le variazioni di un fenomeno nel tempo o nello spazio

Vuoi sapere tutto sui numeri indice semplici a base fissa e mobile, sui numeri indice complessi dei prezzi e delle quantità di Laspeyres e Paashe e sulle loro proprietà? A fine pagina trovi il link al formulario completo!

I numeri indice semplici a base fissa e mobile

Sia X un carattere quantitativo (o variabile quantitativa) osservato su N unità statistiche e siano x₁, x₂,…, x_N le osservazioni, supposte positive; le unità statistiche possono essere tempi (giorni, mesi, anni, ecc.) o luoghi (nazioni, regioni, città, ecc.):

• Il j-esimo numero indice semplice a base fissa s (1≤j≤N) è:

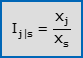
• Il j-esimo numero indice semplice a base mobile (2≤j≤N) è:

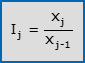Spesso, per ragioni di migliore leggibilità, il valore dei numeri indice viene moltiplicato per 100.

A ciascun numero indice corrisponde un tasso di variazione che aiuta ad interpretare l’indice:

• tasso di variazione = numero indice – 1

(se il numero indice è stato moltiplicato per 100, si sottrae 100 invece di 1). Tale tasso esprime la variazione relativa o percentuale di X tra s e j (per gli indici a base s) o tra j-1 e j (per gli indici a base mobile). I numeri indice, coincidendo con i tassi di variazione a meno della costante unitaria, si interpretano allo stesso modo.

E’ agevole trasformare una serie di numeri indice a base s in una serie a base t, oppure una serie a base fissa s in una a base mobile o viceversa:

• Formula di passaggio dalla base s alla base t:

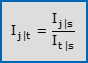
• Formula di passaggio dalla base s alla base mobile:

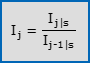
• Formula di passaggio dalla base mobile alla base s:

I numeri indice (complessi) dei prezzi a base fissa

Si consideri un paniere di M beni. Sia X_m il prezzo del bene m (m=1,2,…,M) osservato in N tempi e siano x_m1, x_m2,…, x_mN le osservazioni.

• Il j-esimo numero indice complesso dei prezzi a base fissa s, definito tramite il metodo delle somme ponderate (o metodo degli aggregati di valore) è:

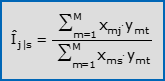dove y_1t, y_2t,…, y_Mt sono quantità dei beni nel paniere ad un fissato tempo t.

• Il j-esimo numero indice complesso dei prezzi a base fissa s, definito tramite il metodo della media ponderata dei numeri indice semplici è:

dove p₁, p₂,…, p_M sono pesi (non negativi) assegnati ai beni nel paniere dal sistema di ponderazione degli indici semplici. Scelte alternative dei pesi conducono a numeri indice diversi; di particolare importanza sono gli indici dei prezzi di Laspeyres (sui quali si basa la costruzione degli indici NIC, FOI e IPCA da parte dell’ISTAT) e di Paashe, per i quali si rinvia al formulario.

Login / Registrati
Vai al formulario

I formulari dell’area
STATISTICA DESCRITTIVA
[2] – [3] – [4] – [5] – [6] – [7] – [8]

Vuoi spiegazioni dettagliate sulle formule ed i risultati presentati nel formulario, corredate da esempi, esercizi ed applicazioni? Trovi tutto questo nelle nostre videolezioni sui Rapporti statistici.

                   Videolezioni                    Rapporti statistici

Vuoi preparare un esame di Statistica con MOV? Clicca sul pulsante Cosa devi studiare?, riempi il form ed inviaci il tuo programma: ti suggeriremo un piano di studio basato sui nostri strumenti didattici e calibrato sulle tue esigenze.

Cosa devi studiare?