Probabilità e variabili casuali I

Funzione di ripartizione e funzione (di densità) di probabilità di una variabile casuale

Vuoi sapere tutto sulle definizioni di probabilità e di variabile casuale e sui molti concetti collegati, tra cui quelli di evento, algebra di eventi, assiomi del Calcolo delle Probabilità, funzione di ripartizione e funzione (di densità) di probabilità? A fine pagina trovi il link al formulario completo!

La funzione di ripartizione e la funzione di probabilità di una variabile casuale discreta

Sia S lo spazio campione associato ad un esperimento casuale, cioè l’insieme dei suoi possibili esiti. Sia A(S) una σ-algebra di eventi legati all’esperimento. Sia P una misura di probabilità su A(S), cioè una funzione che ad ogni evento in A(S) associa una probabilità, rispettando gli assiomi del Calcolo. Sia X una variabile casuale, cioè una funzione che ad ogni esito in S associa un numero reale. Sia X(S) il supporto di X, cioè l’insieme dei valori che X può assumere. Supponi che X(S) sia discreto, cioè composto da un numero finito o infinito numerabile di valori. Allora:

• La funzione di ripartizione di X assegna ad ogni numero reale x la probabilità (secondo P) che X assuma un valore minore o uguale ad x:

Per costruzione, F_X risulta crescente “a gradini”, continua a destra, tende a 0 per x che tende a -∞ e tende ad 1 per x che tende a +∞.

• La funzione di probabilità di X assegna ad ogni valore x_j∈X(S) la probabilità (secondo P) che X assuma tale valore:

Per costruzione, f_X risulta non negativa e la somma di tutti i suoi valori dà 1.

I valori della funzione di probabilità rappresentano l’altezza dei gradini della funzione di ripartizione. Quindi sempre possibile ricavare la prima dalla seconda (per differenza)…

e, viceversa, la seconda dalla prima (per somma):

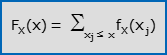
La funzione di ripartizione e la funzione di densità di probabilità di una variabile casuale continua

Nelle stesse ipotesi e con le stesse notazioni del caso discreto, supponi adesso che X(S) sia continuo. Per concretezza, supponi coincida con l’insieme dei numeri reali o con un intervallo, anche illimitato, di numeri reali.

• La funzione di ripartizione di X assegna ad ogni numero reale x la probabilità (secondo P) che X assuma un valore minore o uguale ad x:

Per costruzione, F_X risulta crescente (ma non necessariamente “a gradini”), continua a destra, tende a 0 per x che tende a -∞ e tende ad 1 per x che tende a +∞. Se F_X è anche continua a sinistra – e dunque globalmente continua – la variabile casuale X si dice continua.

• La funzione di densità di probabilità di X è definita sui numeri reali, è non negativa e per ogni x il suo integrale tra -∞ ed x restituisce il valore della funzione di ripartizione in x:

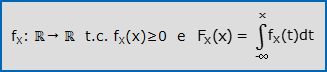La funzione di densità di probabilità è spesso denominata funzione di densità o semplicemente densità di X. Non tutte le variabili casuali continue hanno la densità; quelle che ce l’hanno si dicono assolutamente continue; per esse, tramite la densità si può ricostruire la funzione di ripartizione (per definizione di f_X); se poi f_X è continua, è anche possibile il passaggio contrario, derivando F_X:

Login / Registrati
Vai al formulario

I formulari dell’area
PROBABILITA’
[1] – [2] – [3] – [4]

Vuoi spiegazioni dettagliate sulle formule ed i risultati presentati nel formulario, corredate da esempi, esercizi ed applicazioni? Trovi tutto questo nelle nostre videolezioni su Probabilità e variabili casuali (I parte).

                   Videolezioni                    Probabilità e variabili casuali (I parte)

Vuoi preparare un esame di Statistica con MOV? Clicca sul pulsante Cosa devi studiare?, riempi il form ed inviaci il tuo programma: ti suggeriremo un piano di studio basato sui nostri strumenti didattici e calibrato sulle tue esigenze.

Cosa devi studiare?