L’aggiornamento della probabilità delle cause tramite il teorema di Bayes
Vuoi sapere tutto sulla probabilità condizionata, sulle proprietà della probabilità – tra cui la regola del prodotto, la formula della probabilità totale ed il teorema di Bayes – ma anche sulle variabili casuali multiple e sulla convergenza delle successioni di variabili casuali? A fine pagina trovi il link al formulario completo!
Le formule della probabilità condizionata e della probabilità totale
Siano: S lo spazio campione associato ad un esperimento casuale, cioè l’insieme dei possibili esiti dell’esperimento; A(S) una σ-algebra di eventi legati all’esperimento; P una misura di probabilità su A(S), cioè una funzione che ad ogni evento in A(S) associa una probabilità, rispettando gli assiomi del Calcolo; E ed F eventi di A(S). Allora:
- La probabilità di E condizionata ad F è la probabilità che si verifichino sia E che F, divisa per la probabilità che si verifichi F (si assume P(F)>0):
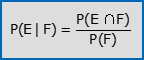
- Direttamente dalla definizione di probabilità condizionata segue la formula della probabilità composta (si assume P(E)>0 e P(F)>0):
![]()
- Se gli eventi F1, F2,…, Fn hanno tutti probabilità positiva e formano una partizione di S (cioè almeno uno di tali eventi si verificherà senz’altro e non più di uno), vale la formula della probabilità totale:
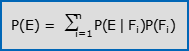 Questo risultato si dimostra scrivendo P(E) = P(E∩S) = P[E∩(∪Fi)] = P[∪(E∩Fi)] = ΣP(E∩Fi) ed applicando agli addendi nell’ultima sommatoria la formula della probabilità composta.
Questo risultato si dimostra scrivendo P(E) = P(E∩S) = P[E∩(∪Fi)] = P[∪(E∩Fi)] = ΣP(E∩Fi) ed applicando agli addendi nell’ultima sommatoria la formula della probabilità composta.
Il teorema di Bayes
Nelle stesse ipotesi che soggiacciono alla formula della probabilità totale ed assumendo, inoltre, che E sia un evento con probabilità positiva, vale la seguente formula di Bayes:
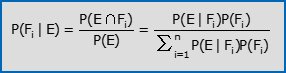 La prima uguaglianza segue dalla definizione di probabilità condizionata; la seconda segue, per il numeratore, dalla formula della probabilità composta e per il denominatore dalla formula della probabilità totale. Nell’ambito del teorema di Bayes, le probabilità che intervengono nella formula prendono nomi specifici:
La prima uguaglianza segue dalla definizione di probabilità condizionata; la seconda segue, per il numeratore, dalla formula della probabilità composta e per il denominatore dalla formula della probabilità totale. Nell’ambito del teorema di Bayes, le probabilità che intervengono nella formula prendono nomi specifici:
- P(Fi) è la probabilità a priori di Fi
- P(Fi|E) è la probabilità a posteriori di Fi
- P(E|Fi) è la verosimiglianza di E (relativamente ad Fi)
L’interpretazione classica del teorema di Bayes è la seguente: posto che E sia un effetto determinabile da una ed una sola di n possibili cause F1, F2,…, Fn, la probabilità che si sia manifestata proprio la causa Fi si può aggiornare, dopo aver osservato E, moltiplicando la sua probabilità prima di osservare E, cioè P(Fi), per la probabilità che E si manifesti in presenza di quella causa, cioè P(E|Fi). La sommatoria a denominatore della formula è un fattore di scala che riproporziona il numeratore in modo che le probabilità a posteriori diano somma 1.
Login / Registrati
Vai al formulario
I formulari dell’area
PROBABILITA’
[1] – [2] – [3] – [4]
Vuoi spiegazioni dettagliate sulle formule ed i risultati presentati nel formulario, corredate da esempi, esercizi ed applicazioni? Trovi tutto questo nelle nostre videolezioni su Probabilità e variabili casuali (II parte).
Videolezioni Probabilità e variabili casuali (II parte)
Vuoi preparare un esame di Statistica con MOV? Clicca sul pulsante Cosa devi studiare?, riempi il form ed inviaci il tuo programma: ti suggeriremo un piano di studio basato sui nostri strumenti didattici e calibrato sulle tue esigenze.
