Integrazione per parti, per sostituzione e per funzioni composte
Vuoi sapere tutto sull’integrazione per parti e sulle altre tecniche di calcolo degli integrali, nonché sul concetto di integrale e sui teoremi ad esso collegati? A fine pagina trovi il link al formulario completo!
La formula di integrazione per parti si ricava dalla regola di derivazione del prodotto di due funzioni.
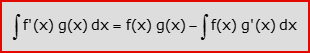In pratica, l’integrazione per parti consente di “scambiare” il segno di derivata nelle funzioni integrande. Se si scelgono opportunamente le funzioni f e g, l’integrale a secondo membro risultarà più agevole da calcolare.
Un’altra formula molto nota è quella di integrazione per sostituzione, che si ricava dalla regola di derivazione di funzioni composte.
Scegliendo opportunamente la sostituzione x=g(t), l’integrale a secondo membro risulterà più semplice di quello a primo membro. A dire il vero, il formalismo della formula non è del tutto rigoroso e lo si è scelto solo per ragioni di semplicità. Infatti, l’integrale a secondo membro darà luogo ad una primitiva, diciamo H(t), nella variabile t, mentre quella cercata è ovviamente nella variabile x. Per completare il calcolo, sarà necessaria la sostituzione t=g-1(x), così che la primitiva cercata sarà H(g-1(x)). Questa osservazione evidenzia il fatto che la funzione x=g(t) deve essere invertibile.
Leggendo la formula precedente in direzione opposta, si ottiene una terza formula che chiameremo di integrazione per funzioni composte. Se F(x) è una primitiva di f(x) (cioè F'(x)=f(x)), allora:
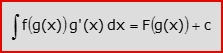
Nota che, sebbene la formula sia strutturalmente analoga a quella di integrazione per sostituzione (e la si dimostra, in effetti, allo stesso modo), in questo caso non è necessario che la funzione g(x) sia invertibile.
Le formule di integrazione per parti, per sostituzione e per funzioni composte, insieme a quelle per l’integrazioni di funzioni razionali fratte, consentono di “calcolare” molti integrali indefiniti, ovvero di esprimerli in termini di funzioni elementari.
Login / Registrati
Vai al formulario
I formulari dell’area
INTEGRALI E SERIE
[1] – [2] – [3]
Vuoi spiegazioni dettagliate sulle formule ed i risultati presentati nel formulario, corredate da esempi, esercizi ed applicazioni? Trovi tutto questo nelle nostre videolezioni sugli Integrali (I parte).
Videolezioni Integrali (I parte)
Vuoi preparare un esame di Matematica con MOV? Clicca sul pulsante Cosa devi studiare?, riempi il form ed inviaci il tuo programma: ti suggeriremo un piano di studio basato sui nostri strumenti didattici e calibrato sulle tue esigenze.