Una star irrazionale: il numero e di Nepero
Vuoi sapere tutto sul numero di Nepero, sulle successioni numeriche e sui loro limiti? A fine pagina trovi il link al formulario completo!
Il numero di Nepero come limite di successione
Il numero di Nepero (o di Eulero), universalmente denotato con la lettera e, gode di notevoli proprietà e si incontra in molti problemi di Matematica teorica ed applicata; vale circa 2,718 e si può definire come limite di una particolare successione:
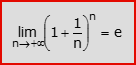Affinché la definizione sia ben posta, occorre provare che il limite della successione an=[1+(1/n)]nesiste finito; i passaggi essenziali della dimostrazione sono:
- Si prova che an è una successione monotona (in particolare, crescente: an ≥ an-1 per ogni n)
- Dal teorema di esistenza del limite di successioni monotone, si conclude che anammette limite
- Si prova che an è una successione limitata (esiste M>0 tale che an<M per ogni n)
- Si conclude che an non può divergere e dunque necessariamente converge (ammette limite finito)
Il valore di convergenza di an è, per definizione, il numero e. Lo si può definire anche come valore di convergenza della serie di termine generale 1/n! .
Le proprietà del numero di Nepero
Alcune delle sue proprietà più significative sono:
- Il numero di Nepero è irrazionale trascendente
- Il numero di Nepero compare nella formula di Eulero eix= cos(x) + i·sin(x) e nella identità di Eulero eiπ+1=0 che è stata definita “l’equazione più bella di tutta la Matematica” in quanto in essa figurano i 4 numeri più importanti (1, 0, e, π)
- La funzione esponenziale avente per base il numero di Nepero, f(x)=ex, è invariante per derivazione (f'(x)=f(x)) e per integrazione indefinita (∫f(x)dx = f(x)+k)
Login / Registrati
Vai al formulario
I formulari dell’area
FUNZIONI, LIMITI, CONTINUITA’
[1] – [2] – [3] – [4] – [5]
Vuoi spiegazioni dettagliate sulle formule ed i risultati presentati nel formulario, corredate da esempi, esercizi ed applicazioni? Trovi tutto questo nelle nostre videolezioni sui Limiti di successioni.
Videolezioni Limiti di successioni
Vuoi preparare un esame di Matematica con MOV? Clicca sul pulsante Cosa devi studiare?, riempi il form ed inviaci il tuo programma: ti suggeriremo un piano di studio basato sui nostri strumenti didattici e calibrato sulle tue esigenze.