Il prodotto cartesiano e le relazioni tra insiemi
Vuoi sapere tutto sul prodotto cartesiano di insiemi, sulle relazioni tra insiemi, su altre operazioni insiemistiche, sui concetti di insieme, sottoinsieme e sulla loro rappresentazione? A fine pagina trovi il link al formulario completo!
Il prodotto cartesiano tra 2 insiemi e la generalizzazione ad n insiemi
Dati due insiemi A e B, gli elementi a∈A e b∈B formano una coppia ordinata (a,b) se l’ordine in cui sono elencati nella coppia è rilevante; ovvero, se (a,b)≠(b,a). Il prodotto cartesiano A×B si definisce come l’insieme di tutte le coppie ordinate il cui primo elemento appartiene ad A ed il cui secondo elemento appartiene a B:
Più in generale, dati n insiemi A1, A2,…, An, gli elementi a1∈A1, a2∈A2,…, an∈An formano una ennupla (o n-pla) ordinata (a1, a2,…, an) se l’ordine in cui sono elencati nella n-pla è rilevante. Il prodotto cartesiano A1×A2×…×An si definisce come l’insieme di tutte le n-pla ordinate il cui primo elemento appartiene ad A1, il cui secondo elemento appartiene ad A2,…, il cui n-esimo elemento appartiene ad An:
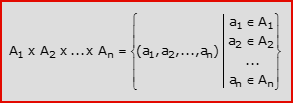Le relazioni di equivalenza e d’ordine
Un qualsiasi sottoinsieme R del prodotto cartesiano A×B è una relazione tra A e B. Diremo che a è in relazione con b, scrivendo aRb, se (a,b)∈R. Un caso particolare interessante si ha quando A=B, cioè quando R è un sottoinsieme del prodotto cartesiano tra A ed A stesso: R⊆A×A. Si possono individuare, allora, alcune relazioni particolarmente importanti, tra cui:
- Relazione di equivalenza (R ha le proprietà dell’essere uguale a in un insieme numerico):
- Relazione d’ordine largo (R ha le proprietà dell’essere maggiore o uguale in un insieme numerico):
- Relazione d’ordine stretto (R ha le proprietà dell’essere maggiore di in un insieme numerico):
- Relazione d’ordine totale:
Login / Registrati
Vai al formulario
I formulari dell’area
INSIEMI E NUMERI
[1] – [2] – [3]
Vuoi spiegazioni dettagliate sulle formule ed i risultati presentati nel formulario, corredate da esempi, esercizi ed applicazioni? Trovi tutto questo nelle nostre videolezioni sugli Insiemi.
Vuoi preparare un esame di Matematica con MOV? Clicca sul pulsante Cosa devi studiare?, riempi il form ed inviaci il tuo programma: ti suggeriremo un piano di studio basato sui nostri strumenti didattici e calibrato sulle tue esigenze.