La derivata di una funzione: definizione e regole di calcolo
Vuoi sapere tutto sul concetto di derivata prima di una funzione e sulle sue applicazioni nell’ambito del Calcolo Differenziale? A fine pagina trovi il link al formulario completo!
La definizione
Il concetto di derivata di una funzione è al centro del Calcolo Differenziale; ne abbiamo già discusso in un precedente articolo su MOV (clicca qui) su MOV. Si lega indissolubilmente al concetto di limite di funzione (clicca qui), che gioca un ruolo di primo piano fin dalla definizione; infatti una funzione f, definita in un dominio Df ed a valori reali, si dice derivabile in un punto x0∈Df se esiste finito il limite per h che tende a 0 del rapporto incrementale di f in x0:
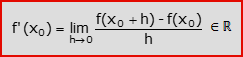 In tal caso il numero f'(x0) si chiama derivata prima di f in x0. Se nel limite precedente si fa tendere h a 0 da sinistra (ossia da valori negativi), si ottiene la definizione di funzione derivabile da sinistra:
In tal caso il numero f'(x0) si chiama derivata prima di f in x0. Se nel limite precedente si fa tendere h a 0 da sinistra (ossia da valori negativi), si ottiene la definizione di funzione derivabile da sinistra:
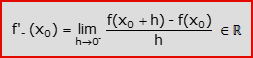 e di derivata sinistra di f in x0, denotata con f’–(x0). Se invece si fa tendere h a 0 da destra (ossia da valori positivi), si ottiene la definizione di funzione derivabile da destra:
e di derivata sinistra di f in x0, denotata con f’–(x0). Se invece si fa tendere h a 0 da destra (ossia da valori positivi), si ottiene la definizione di funzione derivabile da destra:
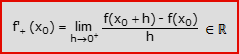 e di derivata destra di f in x0, denotata con f’+(x0). Dalle proprietà del limite di funzione segue che f è derivabile in x0 se e solo se entrambe le derivate sinistra e destra in x0 esistono e coincidono, nel qual caso il loro valore comune sarà anche il valore della derivata di f in x0:
e di derivata destra di f in x0, denotata con f’+(x0). Dalle proprietà del limite di funzione segue che f è derivabile in x0 se e solo se entrambe le derivate sinistra e destra in x0 esistono e coincidono, nel qual caso il loro valore comune sarà anche il valore della derivata di f in x0:
![]() La funzione f si dice derivabile in un intervallo aperto (a,b) se ammette derivata in ogni punto di (a,b); si dice derivabile in un intervallo chiuso [a,b] se è derivabile in (a,b) ed ammette derivata destra in a e sinistra in b.
La funzione f si dice derivabile in un intervallo aperto (a,b) se ammette derivata in ogni punto di (a,b); si dice derivabile in un intervallo chiuso [a,b] se è derivabile in (a,b) ed ammette derivata destra in a e sinistra in b.
Le regole di calcolo
La funzione f’ che ad ogni punto di derivabilità di f associa il valore della derivata nel punto, si dice funzione derivata di f. Nel caso f sia somma, prodotto, quoziente, composizione di altre funzioni, f’ si può calcolare attraverso le seguenti regole di derivazione:
- Per la somma di due funzioni, si ha:
![]()
- Per il prodotto di due funzioni si ha:
![]()
- Per il quoziente di due funzioni (g(x)≠0):
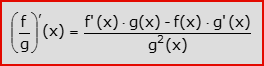
- Per la composizione di due funzioni (f derivabile in g(x)):
![]() Login / Registrati
Login / Registrati
Vai al formulario
I formulari dell’area
CALCOLO DIFFERENZIALE
[1] – [2] – [3]
Vuoi spiegazioni dettagliate sulle formule ed i risultati presentati nel formulario, corredate da esempi, esercizi ed applicazioni? Trovi tutto questo nelle nostre videolezioni sulle Derivate (I parte).
Videolezioni Derivate (I parte)
Vuoi preparare un esame di Matematica con MOV? Clicca sul pulsante Cosa devi studiare?, riempi il form ed inviaci il tuo programma: ti suggeriremo un piano di studio basato sui nostri strumenti didattici e calibrato sulle tue esigenze.
