Le basi del ragionamento matematico: i connettivi logici tra proposizioni
Vuoi sapere tutto sui connettivi logici, sulle loro proprietà, sull’equivalenza tra formule, su tautologia e contraddizione e su altri concetti fondamentali della Logica matematica? A fine pagina trovi il link al formulario completo!
La definizione dei connettivi logici tramite le tavole di verità
Siano p e q due proposizioni logiche, ossia due affermazione alle quali è possibile attribuire un valore di verità (V = vero, oppure F = falso). L’attribuzione può avvenire su basi oggettive o soggettive ma deve essere concettualmente sensata: ad esempio, non sono proposizioni logiche quelle interrogative o esclamative, perché ad esse non si può attribuire un valore di verità. A partire da p e q, si possono costruire altre proposizioni utilizzando dei connettivi logici, definiti attraverso le corrispondenti tavole di verità. Ad esempio:
- Congiunzione “e” (connettivo logico ∧): è definita dalla tavola di verità

- Disgiunzione “o” (connettivo logico ∨): è definita dalla tavola di verità

- Implicazione “se…allora…” (connettivo logico ⇒): è definita dalla tavola di verità
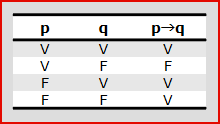 Nell’ambito della Logica matematica, è possibile combinare tra loro questi ed altri connettivi logici per costruire proposizioni più complesse, in cui valori di verità possono essere determinati – in funzione di quelli delle proposizioni elementari – applicando in sequenza le tavole di verità dei singoli connettivi coinvolti.
Nell’ambito della Logica matematica, è possibile combinare tra loro questi ed altri connettivi logici per costruire proposizioni più complesse, in cui valori di verità possono essere determinati – in funzione di quelli delle proposizioni elementari – applicando in sequenza le tavole di verità dei singoli connettivi coinvolti.
Le proprietà dei connettivi logici
I connettivi logici godono di numerose proprietà; ad esempio:
- Congiunzione e disgiunzione sono commutative:
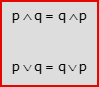
- La congiunzione è distributiva rispetto alla disgiunzione (e viceversa; r è un’altra proposizione):
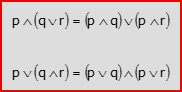
Queste ed altre analoghe proprietà si dimostrano provando che la tavola di verità della proposizione a primo membro, coincide con la tavola di verità della proposizione a secondo membro (formule equivalenti).
Login / Registrati
Vai al formulario
I formulari dell’area
LOGICA
[1] – [2]
Vuoi spiegazioni dettagliate sulle formule ed i risultati presentati nel formulario, corredate da esempi, esercizi ed applicazioni? Trovi tutto questo nelle nostre videolezioni sulla Logica matematica.
Videolezioni Logica matematica
Vuoi preparare un esame di Matematica con MOV? Clicca sul pulsante Cosa devi studiare?, riempi il form ed inviaci il tuo programma: ti suggeriremo un piano di studio basato sui nostri strumenti didattici e calibrato sulle tue esigenze.
