Il concetto di limite di una funzione è alla base dello studio del suo andamento agli estremi del dominio ed interviene nella definizione di molti concetti chiave dell’Analisi Matematica
Il concetto di limite di una funzione è centrale in Analisi Matematica ed in particolare nel Calcolo Infinitesimale. Lo è per varie ragioni.
La ricerca degli asintoti di una funzione
Calcolando il limite di una funzione è possibile studiarne con relativa facilità il comportamento quando la variabile indipendente diventa molto grande (in modulo) o molto vicina a valori esclusi dal dominio; ciò consente di determinare anche gli eventuali asintoti (orizzontali, verticali, obliqui) della funzione. Ad esempio, potresti chiederti come si comporta la funzione:
![]()
quando la variabile x diventa (i) positiva e molto grande oppure (ii) negativa e molto grande in modulo; o ancora quando si avvicina molto (iii) ad 1 (da valori più grandi) ovvero (iv) a -1 (da valori più piccoli), posto che 1 e -1 sono punti di frontiera del dominio di f(x) (la funzione, infatti, non esiste nell’intervallo (-1,1)). Le risposte si ottengono calcolando i seguenti limiti di funzione:
![]()
La simbologia sub (i) dice che “il limite di f(x), per x che tende a più infinito, vale 1”, ossia che quando x diventa positiva e “molto grande”, il valore di f(x) diventa “molto vicino” ad 1; le espressioni virgolettate andrebbero in effetti precisate (quanto “grande”? quanto “vicino”?), ma il senso è quello; le altre simbologie si leggono e si interpretano in maniera analoga. Lasciamo stare, qui, le modalità di calcolo di questi limiti – peraltro piuttosto semplici – e concentriamoci sul loro risvolto grafico:
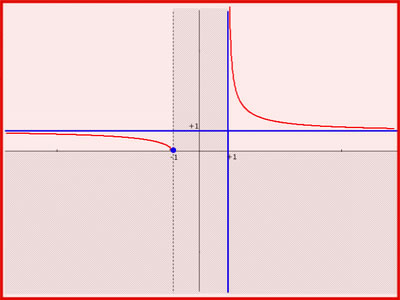
Quando x tende a più o meno infinito, f(x) tende ad 1; quando x tende a +1, f(x) tende a più infinito; quando x tende a -1, f(x) tende a 0.
La curva rossa rappresenta il grafico di f(x); se ne deduce facilmente che (i) quando x diventa positiva e molto grande, la funzione tende ad adagiarsi, “da sopra”, sulla retta y=1, senza peraltro mai toccarla; diremo allora che y=1 è un asintoto orizzontale della funzione per x che tende a più infinito; (ii) quando x diventa negativa e molto grande in modulo, la funzione tende ugualmente ad adagiarsi sulla retta y=1, stavolta “da sotto”, per cui y=1 è un asintoto orizzontale di f(x) anche per x che tende a meno infinito; (iii) quando x si avvicina ad 1 (da valori più grandi), la funzione tende a crescere sempre di più, accostandosi alla retta x=1, senza peraltro mai toccarla; diremo allora che x=1 è un asintoto verticale della funzione per x che tende ad 1+; infine (iv) quando x si avvicina a -1 (da valori più piccoli), la funzione tende a 0, senza peraltro mai raggiungerlo (in x=0 la funzione non esiste). Come si vede, in ciascun caso il limite di funzione descrive perfettamente il comportamento di f(x) che si deduce dal suo grafico; l’espressione analitica ha sempre la sua controparte geometrica!
Per un esempio di asintoto obliquo considera la funzione:
![]()
il cui grafico è riportato, in rosso, qui sotto:
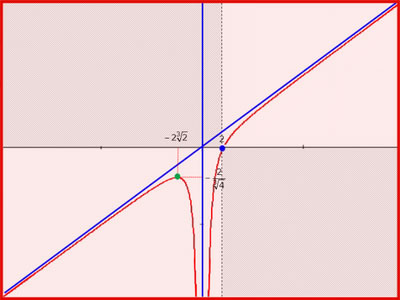
Quando x tende a più o meno infinito, f(x) tende all’infinito adagiandosi sulla retta y=x; quando x tende a 0, f(x) tende a meno infinito.
Se ne deduce, tra l’altro, che:
![]()
Il primo limite di funzione ti dice che quando x diventa positiva e molto grande, f(x) tende a crescere indefinitamente; il secondo ti dice che il modo di crescere di f(x) tende man mano ad assomigliare a quello della retta y=x (la bisettrice del I e III quadrante, che in figura è tracciata in blu), tant’è che la distanza f(x)-x tende ad azzerarsi; diremo allora che y=x è un asintoto obliquo della funzione per x che tende a più infinito (nota che lo è anche per x che tende a meno infinito).
È interessante rimarcare il legame tra limite di una funzione e nozione di infinito. In Matematica, la parola “infinito” non si riferisce ad un numero, bensì alla “grandezza” di un insieme o al comportamento di una variabile; in particolare, il comportamento della variabile y=f(x) che consiste nel superare qualsiasi soglia fissata (per quanto grande!) scegliendo x sufficientemente vicino ad un x0, si sintetizza dicendo che y=f(x) tende ad infinito per x che tende ad x0 e si definisce rigorosamente come:
![]()
Pur non essendo numeri, nel mondo dei limiti di funzione, gli infiniti si possono sommare, moltiplicare e dividere, anche se il risultato non è sempre ovvio – specie quando l’operazione dà luogo a forme indeterminate – e non è sempre un altro infinito. Pensa a due funzione f(x) e g(x) che tendono a +∞ per x che tende ad x0; allora anche la funzione prodotto f(x)∙g(x) tenderà a +∞ ed in questo senso si potrà scrivere (+∞)∙(+∞) = +∞; analogamente, tenderà a +∞ la funzione somma f(x)+g(x) e quindi si potrà scrivere (+∞)+(+∞) = +∞; non è ovvio invece il comportamento delle funzioni differenza f(x)-g(x) e quoziente f(x)/g(x); per dire, nel primo esempio di questa nota abbiamo visto un rapporto tra due infiniti che tende ad 1, mentre nel secondo esempio ne abbiamo visto uno che tende a +∞; il diverso comportamento si deve alla velocità relativa con cui divergono le funzioni a rapporto, che nel primo esempio è la stessa mentre nel secondo è a vantaggio della funzione a numeratore (x3-8 è “più veloce” di x2).
Continuità, derivabilità ed altri concetti legati a quello di limite
La centralità del limite di una funzione nel Calcolo Infinitesimale, comunque, si deve soprattutto al fatto che i concetti più importanti del Calcolo – dalla continuità alla derivata, dall’integrale alla serie – si definiscono attraverso il limite; l’intero edificio del Calcolo Infinitesimale crollerebbe se la nozione di limite di funzione – o quelle insiemistiche sulle quali si basa – venisse meno. Ad esempio, una funzione f(x) sarà continua in un punto x0 se:
![]()
Sarà invece derivabile in x0 se esiste ed è un numero il limite:
![]()
con il che si formalizza l’idea che esiste la retta tangente al grafico della funzione nel punto (x0, f(x0)) (linea blu continua nella figura seguente) e che essa è definita come “limite” della retta che taglia il grafico nei punti (x0, f(x0)) ed (x, f(x)) (linea blu tratteggiata):
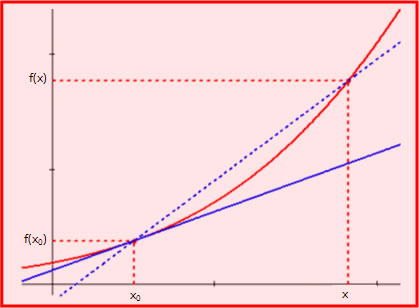
Se il limite della pendenza della retta secante, per x che tende ad x0, esiste finito, allora esiste la retta tangente al grafico della funzione in (x0, f(x0)).
Definizione e calcolo del limite di una funzione
Anche se il limite di una funzione ha un significato sostanziale chiaro, la sua definizione – quella matematicamente rigorosa – non è banale. Proprio per questo su MOV dedichiamo la videolezione:
ad un’introduzione intuitiva ed essenzialmente grafica del limite di una funzione, un po’ come si è fatto finora in questa nota; e solo in una seconda videolezione ci si concentra sulla definizione rigorosa. Quest’ultima, peraltro, spesso si rivela poco utile per calcolare il valore del limite; per questo scopo sono più importanti le proprietà che specificano le operazioni possibili con i limiti di funzione, alcuni teoremi (come il teorema del confronto e il teorema dei carabinieri), la conoscenza di alcuni limiti di funzione ricorrenti – e per questo detti limiti notevoli – ed una lunga serie di “trucchi del mestiere” che aiutano a manipolare la funzione in modo da agevolare il calcolo del limite; di questi trucchi si dà conto nella videolezione:
Esercizi sui Limiti di funzioni
tra le più lunghe del videocorso proprio per l’ampia varietà di casi che si possono incontrare. Qui riporto un esempio, che tra l’altro illustra come vengono spiegati gli esercizi sui limiti di funzione su MOV.
Un esempio di calcolo del limite di una funzione
Vuoi calcolare il seguente limite di funzione:
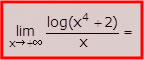
Nota, in primo luogo, che le funzioni a numeratore e denominatore sono infiniti:
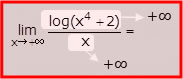
Hai a che fare con una forma indeterminata del tipo ∞/∞; il calcolo del limite non è immediato perché non è chiaro quale delle due funzioni tenda ad infinito più rapidamente e prevalga, dunque, sull’altra. L’idea è manipolare l’espressione in modo da ricondurti ad un limite “facile” da calcolare o comunque noto; considera i seguenti passaggi:
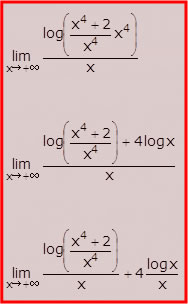
Nel primo, l’argomento del logaritmo è stato diviso e moltiplicato per x4; nel secondo, usando due note proprietà – log(a∙b)=log(a)+log(b) e log(ab)=b∙log(a) – il logaritmo di un prodotto è stato scomposto nella somma di due logaritmi; infine, nel terzo passaggio, la x al denominatore è stata distribuita tra i due addendi al numeratore. Cosa hai guadagnato da queste manipolazioni?
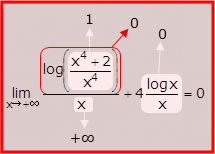
Beh, hai ricondotto il limite iniziale ad uno più facile da calcolare! Come mostra la figura precedente, l’argomento del prima logaritmo tende ad 1, cioè al rapporto tra i coefficienti dei termini di grado più alto, perché i polinomi x4+2 ed x4 divergono alla stessa velocità; di conseguenza, il logaritmo tende a 0 (ricorda che log(1)=0 e log(x) è una funzione continua); questo spinge verso lo 0 la prima frazione, comportamento rafforzato dal fatto che il suo denominatore tende a +∞. La seconda frazione, d’altra parte, è un limite notevole, uno di quelli che bisogna conoscere per risolvere esercizi sui limiti di funzione; il suo valore è 0, conseguenza del fatto che la funzione al denominatore, x, è più veloce di quella al numeratore, log(x). Poiché entrambe le frazioni hanno limite 0, il valore del limite che stai cercando è 0.
Vuoi preparare un esame di Matematica con MOV? Clicca sul pulsante Cosa devi studiare?, riempi il form ed inviaci il tuo programma: ti suggeriremo un piano di studio basato sui nostri strumenti didattici e calibrato sulle tue esigenze.
