Le derivate di una funzione

Le derivate ti aiutano a studiare le proprietà locali di una funzione

Il Calcolo Differenziale studia le variazioni del valore f(x) della funzione f, a fronte di variazioni infinitesime della variabile x. Qui sia f(x) che x saranno numeri reali, anche se sono possibili varie generalizzazioni. Lo studio delle variazioni di f(x) a fronte di “piccole” variazioni di x genera metodi potentissimi per studiare alcune proprietà “locali” della funzione, cioè valide (almeno) in un intervallo di valori della x: tratti crescenti/decrescenti, punti di massimo/minimo, tratti concavi/convessi, punti di flesso, sono gli esempi più comuni. I metodi in questione fanno uso delle derivate della funzione.

La derivata prima: definizione e significato geometrico

In una nota precedente (clicca qui) ho ricordato che la definizione di derivabilità di una funzione in un punto x₀ e l’associata nozione di derivata prima in x₀, si basano sul concetto di limite di funzione; in particolare, f sarà derivabile in x₀ se esiste ed è un numero il limite:

La frazione a destra del limite si chiama rapporto incrementale di f in x₀ ed esprime la pendenza della retta secante il grafico di f nei punti P₀=(x₀, f(x₀)) e P=(x, f(x)) (linea blu tratteggiata nella figura seguente). Man mano che x si avvicina ad x₀, P si sposta lungo il grafico di f verso P₀, così che la retta secante si muove “ruotando” intorno a P₀. Se il limite di cui sopra esiste finito, la retta secante diventerà arbitrariamente vicina ad una retta con pendenza pari al valore del limite, ossia alla derivata prima di f in x₀, indicata con f'(x₀): si tratta della retta tangente al grafico della funzione nel punto P₀ (linea blu continua). La sua equazione è:

y = f(x₀)+f'(x₀)(x-x₀)

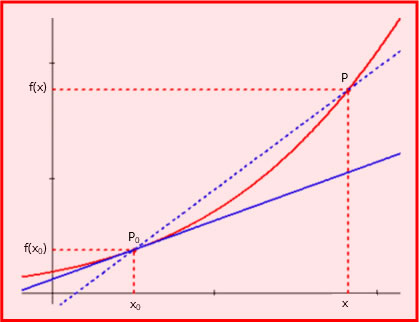
Quando x tende ad x0, la pendenza della retta secante in P e P0 converge alla derivata prima di f in x0, cioè la pendenza della retta tangente in P0

Esistenza della derivata prima in x₀ ed esistenza della retta tangente in P₀ sono dunque concetti equivalenti. La figura precedente evidenzia bene che, in prossimità di x₀, la retta tangente approssima la funzione: i due grafici quasi si sovrappongono! In effetti se in un punto x si approssima il valore della funzione, cioè f(x), con il valore della retta tangente, cioè f(x₀)+f'(x₀)(x-x₀), l’errore che si commette:

E(x) = f(x) – [f(x₀)+f'(x₀)(x-x₀)]

si riduce più velocemente della distanza tra x e x₀; infatti:

L’idea quindi è che quando x si muove nei pressi di x₀, puoi valutare gli effetti sul valore della funzione facendo i conti direttamente sulla retta tangente (che ha una forma analitica più semplice): commetterai un errore, che però puoi sempre “controllare” riducendo la distanza di x da x₀. Questo principio è alla base di numerosi risultati (teoremi, criteri, ecc.) utili a determinare molte proprietà qualitative della funzione; su MOV li abbiamo enunciati e dimostrati nelle videolezioni:

                   Teoria delle                    Derivate (I parte)

Le regole di derivazione

Ora, se ad ogni x nel dominio di f si associa la derivata prima f'(x) (s’intende, dove esiste), otteniamo la funzione derivata prima di f, indicata con f’. In realtà, escluse le funzioni elementari, f'(x) non si ricava direttamente dalla definizione di derivata, bensì applicando alcune regole di derivazione che permettono di calcolare la derivata di somme, prodotti, quozienti, composizioni di funzioni elementari. Nelle videolezioni citate abbiamo dedicato ampio spazio a queste regole e nella videolezione:

                   Esercizi sulle                    Derivate (I parte)

trovi tantissimi esempi; per dire:

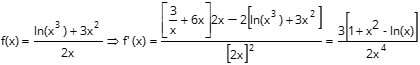
Le derivate successive alla prima si definiscono e si calcolano applicando in modo iterativo le idee appena illustrate. Così, la derivata prima di f’ sarà la derivata seconda di f, indicata con f”; la derivata prima di f” sarà la derivata terza di f, indicata con f”’ o f⁽³⁾; e più in generale, la derivata prima di f^(n-1) sarà la derivata n-esima di f, indicata con f⁽ⁿ⁾. Naturalmente il dominio di queste funzioni derivate potrebbe restringersi man mano che aumenta l’ordine di derivazione; se in un punto x la funzione f ammette derivata n-esima per ogni n, si dirà infinitamente derivabile in quel punto.

Le derivate successive alla prima

Su MOV, le derivate successive alla prima vengono discusse nella videolezione:

                   Teoria delle                    Derivate (II parte)

Sono importanti perché consentono di scoprire con relativa facilità altre proprietà locali della funzione per le quali la derivata prima non è abbastanza informativa; in particolare, lo studio della derivata seconda permette di individuare i tratti dove la funzione è concava, quelli dove è convessa ed i punti dove cambia la concavità (punti di flesso). Inoltre, consentono di migliorare l’approssimazione locale della funzione rispetto a quella offerta dalla retta tangente; per una funzione con derivate fino all’ordine n in un punto x₀ (e che soddisfa qualche altra condizione di “regolarità”), esiste infatti un polinomio di ordine n (polinomio di Taylor) che nei pressi di x₀ approssima la funzione a meno di un errore che si riduce più rapidamente di (x-x₀)ⁿ. Per n=1, il polinomio in questione è la retta tangente; per n=2, è una parabola; per n>2 l’approssimante si complica ma resta pur sempre elementare essendo una somma di potenze di ordine crescente; quindi quando x si muove nei pressi di x₀, puoi valutare gli effetti sul valore della funzione facendo i conti sul polinomio di Taylor e controllare l’errore riducendo la distanza di x da x₀.

Un’applicazione delle derivate ad un problema di Marketing

Le derivate hanno moltissime applicazioni a problemi sia teorici che pratici. Chiudo questa nota con un esempio tratto dal Marketing; esempi tratti dalla Fisica, dalla Geometria, dalla Finanza, dalla Biologia sono presenti nella videolezione sugli Esercizi d’esame già citata (in particolare nell’Esercizio 5) e molti altri sarebbero possibili, in quegli stessi ambiti come in altri.

Immagina di avviare una campagna pubblicitaria al tempo x=0; l’unità di tempo potrebbe essere, diciamo, il giorno. Il costo in euro per prolungare la campagna fino al tempo x>0 è di tipo lineare:

S(x) = K+a·x

dove K>0 è il costo fisso di attivazione della campagna ed a>0 è il costo per mantenerla attiva un giorno (infatti S(x+1)-S(x)=a). Il fatturato, in euro, che prevedi di realizzare entro il tempo x è:

V(x) = M·(1-b·e^-cx)

dove M>0 è il fatturato potenziale; 0<b<1 è la quota di fatturato conquistabile grazie alla pubblicità: infatti v(0)=M-M·b è il fatturato prima di iniziare la campagna e d’altronde, prorogando indefinitamente la campagna (x→∞) il fatturato converge al suo potenziale (V(x)→M), quindi il fatturato generabile con la pubblicità è M·b e la sua quota è b; c>0 è un parametro di efficienza della campagna: maggiore è c (e minore è b), più rapidamente il fatturato si avvicina al suo potenziale M; nota che se c→0, V(x)→V(0) per ogni x, dunque la forma analitica scelta per V(x) sottintende l’ipotesi che dal tempo x=0 in poi, il fatturato può essere incrementato solo con una campagna pubblicitaria efficiente.

Chiama, infine, m il margine di profitto sul fatturato. Il problema, in termini manageriali, è: conviene effettuare la campagna pubblicitaria? Se si, fin quando conviene protrarla?

Il profitto che prevedi al tempo x è:

P(x) = m·V(x)-S(x) = m ·M·(1-b·e^-cx)-K-a·x

Cerchiamo il punto di massimo assoluto di P(x) nell’intervallo [0,∞); lo chiameremo x_max. Tale ricerca si può condurre studiando la derivata prima di P, cioè:

P'(x) = c·m·M·b·e^-cx – a

Si vede facilmente che P'(x) è positiva, nulla e negativa a seconda che x sia, rispettivamente, minore, uguale o maggiore del valore:

che quindi è il punto di massimo di P(x) sull’intera retta reale, cioè sul dominio naturale della funzione P(x); a te però interessa il massimo di P(x) in [0,∞); beh, se l’argomento del logaritmo in x* è minore o uguale a 1, x* sarà minore o uguale a 0, quindi P(x) sarà decrescente in [0,∞) e dunque il suo massimo sarà in x_max=0; in altre parole, se c·m·M·b≤a, non conviene effettuare la campagna pubblicitaria, perché il suo costo “magia” fin da subito i profitti che genera.

Se invece l’argomento del logaritmo in x* è maggiore di 1, x* sarà maggiore di 0, quindi risulterà x_max=x*; ovvero, se c·m·M·b>a, conviene effettuare la campagna pubblicitaria e protrarla fino a x*; ulteriori prolungamenti “mangerebbero” i profitti generati dalla campagna stessa.

È interessante studiare la dipendenza del timing ottimale della campagna, cioè x_max, dai parametri del problema. Si vede subito che x* aumenta al crescere di m, M e b e diminuisce al crescere di a e ciò non sorprende: maggiori sono il margine di profitto, il fatturato potenziale e la quota conquistabile con la pubblicità, più conviene prolungare la campagna; viceversa, più è costoso prorogarla, minore sarà la sua durata ottimale. Il parametro c invece – l’efficienza della campagna – ha un effetto incerto sulla sua durata ottimale; matematicamente, questo deriva dal fatto che c compare in x* sia al numeratore che al denominatore; economicamente, la cosa si spiega col fatto che una campagna molto efficiente, per un verso rende più profittevole un giorno di pubblicità, il che induce a prolungarla; per altro verso, fa si che il fatturato potenziale venga raggiunto rapidamente, il che riduce la durata della campagna (una volta raggiunto il potenziale, la pubblicità diventa solo un costo). Si può valutare con maggior cura l’effetto di c su x* considerando x* come funzione di c, cioè x*(c), e valutando la derivata di questa funzione; si scopre facilmente che x*(c) aumenta finché c·m·M·b<e·a e diminuisce quando c·m·M·b>e·a.

Vuoi preparare un esame di Matematica con MOV? Clicca sul pulsante Cosa studiare?, riempi il form ed inviaci il tuo programma: ti suggeriremo un piano di studio basato sui nostri strumenti didattici e calibrato sulle tue esigenze.

Cosa devi studiare?