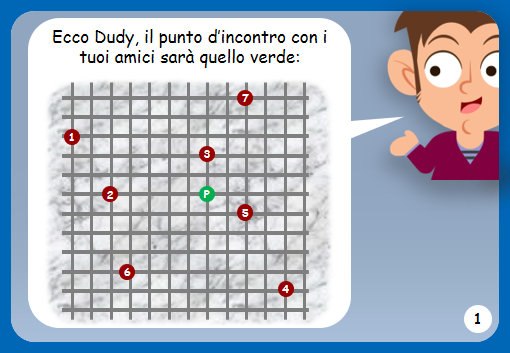
Incontrasi “a metà strada”: punto medio o punto mediano?
Per rivedere il testo del problema clicca qui. Su MOV, nelle nostre videolezioni, abbiamo discusso tutti gli strumenti statistici necessari per risolvere questo problema, inclusi il concetto di mediana, le formule per calcolarla e le sue proprietà più importanti, come quella di minimizzazione della distanza assoluta da un insieme di punti.
Videolezioni Mediana e sue proprietà
LA SOLUZIONE IN SINTESI
LA SOLUZIONE IN DETTAGLIO
La soluzione del quesito si basa su una proprietà notevole della più nota tra le medie di posizione: la mediana. Le medie di posizione servono quando si cerca di posizionare in modo sintetico, cioè con un solo numero, un insieme di dati; oltre alla mediana sono ben noti e largamente utilizzati anche altri quantili, in particolare quartili, decili e percentili. A differenza delle medie analitiche, quelle di posizione non dipendono dal valore dei dati ma solo dalla loro posizione relativa, dal loro ranking nell’insieme considerato; sono quindi robuste rispetto alla presenza di valori anomali (outliers).
La mediana come centro di un insieme di dati
La mediana è un valore che si colloca al centro dell’insieme di dati. Questa affermazione si può intendere i due modi. È al centro nel senso che lascia (circa) metà dei dati alla propria destra e (circa) metà alla propria sinistra: questa è la definizione classica di mediana (nella videolezione sulla Teoria di base viene chiarito il senso di quel “circa” ed introdotta una semplice regola di calcolo). Ma la mediana è al centro dell’insieme di dati anche nel senso che rende minima la distanza totale dai dati: cioè, se collochi i dati su una retta, assimilandoli a punti, sommi le distanze di questi punti da un generico punto C e cerchi di minimizzare tale somma rispetto a C, scopri che il C minimizzante è la mediana (questa proprietà della mediana viene dimostrata in modo rigoroso nella videolezione sui Complementi). Tra l’altro, il ragionamento proposto – qui e nelle videolezioni – si può rovesciare: cioè si può assumere la proprietà enunciata come definizione di mediana e provare che l’indicatore così definito divide l’insieme dei dati in due parti approssimativamente uguali, trasformando la definizione classica in una proprietà. Qualunque sia l’approccio adottato, la proprietà minimizzante della mediana viene utilizzata da Movy per risolvere il problema che Dudy gli ha posto.
Le ipotesi alla base della soluzione proposta
Prima di applicare la proprietà, va notato, osservando la mappa, che tutte le abitazioni degli amici di Dudy sono collegate ad un qualsiasi punto della città mediante strade orizzontali e verticali; sono esclusi spostamenti di altro genere, in particolare diagonali. Questo è decisivo nel definire il concetto di distanza tra il punto d’incontro ed un’abitazione; se fossero ammessi spostamenti diagonali, tale distanza sarebbe quella in linea d’aria ed il problema avrebbe una soluzione diversa, basata su una proprietà della media aritmetica; per approfondimenti su questa variante, puoi vedere l’Esercizio 5 della video-esercitazione.
La restrizione agli spostamenti orizzontali e verticali, invece, fa si che la distanza tra punto d’incontro ed abitazione sia la somma della distanza orizzontale (o longitudinale) e di quella verticale (o latitudinale). Ad esser pignoli, si potrebbe osservare che esistono diversi percorsi che collegano punto d’incontro ed abitazione, tutti equivalenti in quanto a distanze orizzontali e verticali; per assumerli equivalenti anche dal punto di vista della strada effettivamente percorsa, bisogna escludere che vi siano dossi o avvallamenti che allunghino un percorso rispetto ad un altro; ma Movy ha ricevuto da Dudy precise garanzie in tale senso. Ciò posto, la distanza totale che gli amici di Dudy percorreranno per arrivare al punto d’incontro, sarà la somma delle 7 distanze orizzontali dalle abitazioni (denotata con O nel fumetto), più la somma delle 7 distanze verticali (denotata con V).
Soluzione del problema
A questo punto si può davvero applicare la proprietà della mediana ricordata poco fa. Infatti la mediana delle posizioni orizzontali minimizza la somma O e la mediana delle posizioni verticali minimizza la somma V. Il punto d’incontro che ha per coordinate le due mediane, minimizza sia O che V e quindi anche O+V. Il resto è un semplice calcolo, ai fini del quale – nota bene – non rilevano i valori delle 7 posizioni, ma solo il loro ranking; quindi, non c’è alcun bisogno di fissare un sistema di riferimento cartesiano per risolvere il problema, basta ordinare le posizioni delle 7 abitazioni. La mediana sarà il valore centrale delle posizioni ordinate; la soluzione, sia per l’ordinamento orizzontale che per quello verticale, è riportata nel box 3 del fumetto.
Vuoi preparare un esame di Statistica con MOV? Clicca sul pulsante Cosa devi studiare?, riempi il form ed inviaci il tuo programma: ti suggeriremo un piano di studio basato sui nostri strumenti didattici e calibrato sulle tue esigenze.