Risolvere i limiti in forma indeterminata: i limiti notevoli
Vuoi sapere tutto sui limiti notevoli, sulla definizione di limite di funzione, sulle proprietà e sui teoremi collegati ai limiti di funzione? A fine pagina trovi il link al formulario completo!
Il concetto di limite di funzione è al centro del Calcolo Infinitesimale; ne abbiamo già parlato in un precedente articolo qui su MOV (clicca qui). Dal punto di vista operativo, il calcolo dei limiti richiede diversi “ingredienti”: occorre conoscere i limiti delle funzioni elementari, le operazioni possibili con i limiti, alcuni teoremi (in particolare, il teorema dei carabinieri e quello di de L’Hopital) e sicuramente i limiti notevoli, cioè il valore di alcuni limiti molto comuni ai quali si possono ricondurre altri limiti che in partenza si presentano in forma indeterminata.
I principali limiti notevoli
- Limiti legati al confronto tra una funzione logaritmo ed una funzione potenza (a>0, b>0):
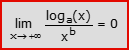
- Limiti legati al confronto tra una funzione logaritmo ed una funzione esponenziale (a>1, b>1):
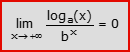
- Limiti legati al confronto tra una funzione potenza ed una funzione esponenziale (a>1, b>0):
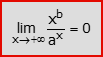
- Altri limiti (e = numero di Nepero, sin(.) = funzione seno, cos(.) = funzione coseno):
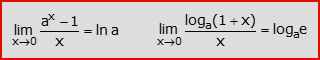
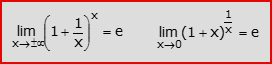Esistono anche altri limiti notevoli ma questi sono certamente i principali. Dimostrarli (soprattutto quelli ricompresi nell’ultimo blocco) può non essere banale, ma in genere nelle prove d’esame scritte, i limiti notevoli possono essere utilizzati senza doverne presentare la dimostrazione: pertanto, non appena si riesce a manipolare il limite da calcolare in modo da ricondurlo ad un limite notevole, se ne può dedurre il risultato senza ulteriori passaggi.
Login / Registrati
Vai al formulario
I formulari dell’area
FUNZIONI, LIMITI, CONTINUITA’
[1] – [2] – [3] – [4] – [5]
Vuoi spiegazioni dettagliate sulle formule ed i risultati presentati nel formulario, corredate da esempi, esercizi ed applicazioni? Trovi tutto questo nelle nostre videolezioni sui Limiti di funzioni.
Videolezioni Limiti di funzioni
Vuoi preparare un esame di Matematica con MOV? Clicca sul pulsante Cosa devi studiare?, riempi il form ed inviaci il tuo programma: ti suggeriremo un piano di studio basato sui nostri strumenti didattici e calibrato sulle tue esigenze.