Gli integrali impropri (o generalizzati) di funzioni continue
Vuoi sapere tutto sugli integrali impropri di funzioni continue ma anche sul calcolo dei volumi dei solidi di rotazione tramite gli integrali? A fine pagina trovi il link al formulario completo!
Gli integrali impropri su intervalli limitati
Sia f(x) una funzione continua su un intervallo limitato, di estremi a e b, non definita in uno di tali estremi. L’integrale di f(x) esteso all’intervallo si definisce allora nel modo seguente:
- Intervallo [a,b) – aperto a destra – ed f(x) non definita in b: l’integrale improprio di f(x) in [a,b) è il limite per h che tende a 0 da destra (cioè da valori positivi) dell’integrale definito di f(x) tra a e b-h
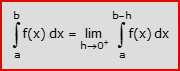
- Intervallo (a,b] – aperto a sinistra – ed f(x) non definita in a: l’integrale improprio di f(x) in (a,b] è il limite per h che tende a 0 da destra (cioè da valori positivi) dell’integrale definito di f(x) tra a+h e b
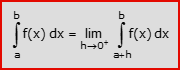
Gli integrali impropri su intervalli illimitati
Sia f(x) una funzione continua su un intervallo illimitato a destra o a sinistra. L’integrale di f(x) esteso all’intervallo si definisce allora nel modo seguente:
- Intervallo [a, +∞): l’integrale improprio di f(x) in [a,+∞) è il limite per b che tende a +∞ dell’integrale definito di f(x) tra a e b
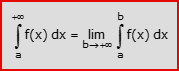
- Intervallo (-∞, b]: l’integrale improprio di f(x) in (-∞,b] è il limite per a che tende a -∞ dell’integrale definito di f(x) tra a e b
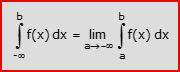
Gli integrali impropri a primo membro nelle precedenti definizioni esistono se esistono i limiti a secondo membro; se uno di tali limiti è finito, il corrispondente integrale improprio si dice convergente; si dice invece divergente se il limite è infinito. Si può dimostrare che se f(x), oltre che continua, è anche non negativa, i suoi integrali impropri definiti nelle precedenti formule esistono, cioè o convergono o divergono; tra i più importanti criteri per stabilire la convergenza o divergenza vi sono quello del confronto e del confronto asintotico.
Login / Registrati
Vai al formulario
I formulari dell’area
INTEGRALI E SERIE
[1] – [2] – [3]
Vuoi spiegazioni dettagliate sulle formule ed i risultati presentati nel formulario, corredate da esempi, esercizi ed applicazioni? Trovi tutto questo nelle nostre videolezioni sugli Integrali (II parte).
Videolezioni Integrali (II parte)
Vuoi preparare un esame di Matematica con MOV? Clicca sul pulsante Cosa devi studiare?, riempi il form ed inviaci il tuo programma: ti suggeriremo un piano di studio basato sui nostri strumenti didattici e calibrato sulle tue esigenze.
