Risolvere x2+2=0: l’insieme dei numeri complessi
Vuoi sapere tutto sui numeri complessi, in forma cartesiana e trigonometrica, e sulle loro proprietà fondamentali? A fine pagina trovi il link al formulario completo!
I numeri complessi in forma cartesiana
L’esistenza di equazioni polinomiali – anche molto semplici, come ad esempio X2+2=0 – che non hanno soluzione tra i numeri reali, motiva l’introduzione dei numeri complessi. Il punto di partenza è il concetto di unità immaginaria i, definita come soluzione dell’equazione i2 = -1 ed indicata con:
![]() Si attribuisce così una connotazione numerica alla radice di -1, che nel campo reale non è definita. Ora, se a e b sono numeri reali, z = a + ib si dirà numero complesso di parte reale a e di parte immaginaria b. Quella appena scritta si dice forma cartesiana di z; è possibile e molto utile scrivere z anche in una forma diversa, detta trigonometrica. L’insieme dei numeri complessi sarà dunque:
Si attribuisce così una connotazione numerica alla radice di -1, che nel campo reale non è definita. Ora, se a e b sono numeri reali, z = a + ib si dirà numero complesso di parte reale a e di parte immaginaria b. Quella appena scritta si dice forma cartesiana di z; è possibile e molto utile scrivere z anche in una forma diversa, detta trigonometrica. L’insieme dei numeri complessi sarà dunque:
![]() Evidentemente, l’unità immaginaria è il numero complesso di parte reale 0 e parte immaginaria 1. Su questi numeri sono definite le comuni operazioni di somma, prodotto e quoziente:
Evidentemente, l’unità immaginaria è il numero complesso di parte reale 0 e parte immaginaria 1. Su questi numeri sono definite le comuni operazioni di somma, prodotto e quoziente:
- Somma di a+ib e a’+ib’:
![]()
- Prodotto di a+ib e a’+ib’:
![]()
- Quoziente di a+ib e a’+ib’ (a≠0 e/o b≠0):
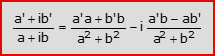 In sostanza, si applicano le note regole di calcolo tra numeri reali ricordando, in più, che i2=-1. La forma trigonometrica dei numeri complessi consente di calcolarne agevolmente anche la potenza n-esima e le radici n-esime. Tali concetti sono di fondamentale importanza per poter enunciare e dimostrare il teorema fondamentale dell’algebra, per il quale ogni equazione polinomiale di variabile complessa di ordine n, ammette n radici complesse, se contate con la loro molteplicità.
In sostanza, si applicano le note regole di calcolo tra numeri reali ricordando, in più, che i2=-1. La forma trigonometrica dei numeri complessi consente di calcolarne agevolmente anche la potenza n-esima e le radici n-esime. Tali concetti sono di fondamentale importanza per poter enunciare e dimostrare il teorema fondamentale dell’algebra, per il quale ogni equazione polinomiale di variabile complessa di ordine n, ammette n radici complesse, se contate con la loro molteplicità.
Login / Registrati
Vai al formulario
I formulari dell’area
INSIEMI E NUMERI
[1] – [2] – [3]
Vuoi spiegazioni dettagliate sulle formule ed i risultati presentati nel formulario, corredate da esempi, esercizi ed applicazioni? Trovi tutto questo nelle nostre videolezioni sui Numeri complessi.
Vuoi preparare un esame di Matematica con MOV? Clicca sul pulsante Cosa devi studiare?, riempi il form ed inviaci il tuo programma: ti suggeriremo un piano di studio basato sui nostri strumenti didattici e calibrato sulle tue esigenze.
