Il Teorema di Weierstrass ed altri teoremi “classici” sulle funzioni continue
Vuoi sapere tutto sul teorema di Weierstrass, sul concetto di funzione continua e sugli altri risultati collegati alla continuità di una funzione? A fine pagina trovi il link al formulario completo!
Sia f(x) una funzione continua nell’intervallo [a,b]; f(x) soddisfa una serie di proprietà importanti espresse in alcuni teoremi “classici” della Analisi Matematica:
- Teorema degli zeri: se f assume valori di segno opposto agli estremi dell’intervallo [a,b], allora ammette almeno uno zero (ovvero si annulla almeno in un punto) in (a,b)
- Teorema dei valori intermedi: f(x) assume tutti i valori compresi tra f(a) e f(b)
- Teorema di Weierstrass: f(x) ammette massimo e minimo assoluti in [a,b]
- Corollario del Teorema di Weierstrass: f(x) assume tutti i valori compresi tra il massimo ed il minimo di f(x) in [a,b]
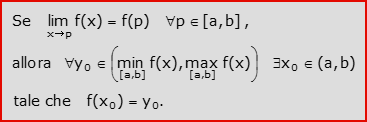Entrambi i risultati principali (Teorema degli zeri e Teorema di Weierstrass) vengono dimostrati attraverso il metodo di bisezione, che può essere impiegato anche per approssimare con precisione arbitraria gli “zeri” di cui si parla nell’omologo teorema. A tale scopo, si divide l’intervallo [a,b] a metà e poi si seleziona un sotto-intervallo dove l’ipotesi del teorema (la funzione assume valori di segno opposto agli estremi dell’intervallo) è ancora soddisfatta e che pertanto contiene uno zero della funzione; iterando la procedura n volte, si ricava un sotto-intervallo di lunghezza Ln = (b-a)/2n e che contiene uno zero della funzione; un qualsiasi valore in questo sotto-intervallo approssima tale zero con un errore inferiore ad Ln; scegliendo n abbastanza grande, si può ridurre Ln fino ad assicurarsi l’approssimazione desiderata.
Login / Registrati
Vai al formulario
I formulari dell’area
FUNZIONI, LIMITI, CONTINUITA’
[1] – [2] – [3] – [4] – [5]
Vuoi spiegazioni dettagliate sulle formule ed i risultati presentati nel formulario, corredate da esempi, esercizi ed applicazioni? Trovi tutto questo nelle nostre videolezioni sulle Funzioni continue.
Videolezioni Funzioni continue
Vuoi preparare un esame di Matematica con MOV? Clicca sul pulsante Cosa devi studiare?, riempi il form ed inviaci il tuo programma: ti suggeriremo un piano di studio basato sui nostri strumenti didattici e calibrato sulle tue esigenze.